- Question 1
- Q1a
- Q1b
- Q1c
- Q1d
- Q1e
- Q1f
- Q1g
- Q1h
- Q1i
DANL 200: Introduction to Data Analytics
DANL 200 - Homework Assignment 5 - Example
Answers
Byeong-Hak Choe
2023-02-14
Loading R packages for Homework Assignment 4
library(tidyverse)
library(lubridate)
library(stargazer)
library(broom)Question 1
The following data is for Question 1.
beer_markets <- read_csv(
'https://bcdanl.github.io/data/beer_markets.csv'
)- Variable description
hh: an identifier of the purchasing household;_purchase_desc: details on the purchased item;quantity: the number of items purchased;brand: Bud Light, Busch Light, Coors Light, Miller Lite, or Natural Light;spent: total dollar value of purchase;beer_floz: total volume of beer, in fluid ounces;price_per_floz: price per fl.oz. (i.e., beer spent/beer floz);container: the type of container;promo: Whether the item was promoted (coupon or otherwise);market: Scan-track market (or state if rural);- demographic data, including gender, marital status, household income, class of work, race, education, age, the size of household, and whether or not the household has a microwave or a dishwasher.
Q1a
Create the data.frame that keeps all the observations whose value of
container is either ‘CAN’ or ‘NON REFILLABLE BOTTLE’ in the
given data.frame, beer_markets.
table(beer_markets$container)##
## CAN KEG KEG BALL
## 53015 118 2
## NON REFILLABLE BOTTLE NON REFILLABLE BOTTLE ALUMINUM NON REFILLABLE BOTTLE PLASTIC
## 19095 186 543
## REFILLABLE BOTTLE
## 156beer_markets <- filter(beer_markets,
container == 'CAN' |
container =='NON REFILLABLE BOTTLE')Q1b
Create the data.frame that has factor-type variables of
container and market using the resulting
data.frame from Q1a.
beer_markets <- beer_markets %>%
mutate(container = factor(container),
market = factor(market))
levels(beer_markets$container)## [1] "CAN" "NON REFILLABLE BOTTLE"levels(beer_markets$market)## [1] "ALBANY" "ATLANTA" "BALTIMORE"
## [4] "BIRMINGHAM" "BOSTON" "BUFFALO-ROCHESTER"
## [7] "CHARLOTTE" "CHICAGO" "CINCINNATI"
## [10] "CLEVELAND" "COLUMBUS" "DALLAS"
## [13] "DENVER" "DES MOINES" "DETROIT"
## [16] "EXURBAN NY" "GRAND RAPIDS" "HARTFORD-NEW HAVEN"
## [19] "HOUSTON" "INDIANAPOLIS" "JACKSONVILLE"
## [22] "KANSAS CITY" "LITTLE ROCK" "LOS ANGELES"
## [25] "LOUISVILLE" "MEMPHIS" "MIAMI"
## [28] "MILWAUKEE" "MINNEAPOLIS" "NASHVILLE"
## [31] "NEW ORLEANS-MOBILE" "OKLAHOMA CITY-TULSA" "OMAHA"
## [34] "ORLANDO" "PHILADELPHIA" "PHOENIX"
## [37] "PITTSBURGH" "PORTLAND, OR" "RALEIGH-DURHAM"
## [40] "RICHMOND" "RURAL ALABAMA" "RURAL ARKANSAS"
## [43] "RURAL CALIFORNIA" "RURAL COLORADO" "RURAL FLORIDA"
## [46] "RURAL GEORGIA" "RURAL IDAHO" "RURAL ILLINOIS"
## [49] "RURAL INDIANA" "RURAL IOWA" "RURAL KANSAS"
## [52] "RURAL KENTUCKY" "RURAL LOUISIANA" "RURAL MAINE"
## [55] "RURAL MICHIGAN" "RURAL MINNESOTA" "RURAL MISSISSIPPI"
## [58] "RURAL MISSOURI" "RURAL MONTANA" "RURAL NEBRASKA"
## [61] "RURAL NEVADA" "RURAL NEW HAMPSHIRE" "RURAL NEW MEXICO"
## [64] "RURAL NEW YORK" "RURAL NORTH CAROLINA" "RURAL NORTH DAKOTA"
## [67] "RURAL OHIO" "RURAL OKLAHOMA" "RURAL OREGON"
## [70] "RURAL PENNSYLVANIA" "RURAL SOUTH CAROLINA" "RURAL SOUTH DAKOTA"
## [73] "RURAL TENNESSEE" "RURAL TEXAS" "RURAL VERMONT"
## [76] "RURAL VIRGINIA" "RURAL WASHINGTON" "RURAL WEST VIRGINIA"
## [79] "RURAL WISCONSIN" "RURAL WYOMING" "SACRAMENTO"
## [82] "SALT LAKE CITY" "SAN ANTONIO" "SAN DIEGO"
## [85] "SAN FRANCISCO" "SEATTLE" "ST. LOUIS"
## [88] "SURBURBAN NY" "SYRACUSE" "TAMPA"
## [91] "URBAN NY" "WASHINGTON DC"table(beer_markets$container)##
## CAN NON REFILLABLE BOTTLE
## 53015 19095table(beer_markets$market)##
## ALBANY ATLANTA BALTIMORE BIRMINGHAM
## 487 1279 374 1137
## BOSTON BUFFALO-ROCHESTER CHARLOTTE CHICAGO
## 872 607 1246 1879
## CINCINNATI CLEVELAND COLUMBUS DALLAS
## 1270 1226 1862 2098
## DENVER DES MOINES DETROIT EXURBAN NY
## 796 716 1731 321
## GRAND RAPIDS HARTFORD-NEW HAVEN HOUSTON INDIANAPOLIS
## 739 370 1673 1213
## JACKSONVILLE KANSAS CITY LITTLE ROCK LOS ANGELES
## 501 663 452 1564
## LOUISVILLE MEMPHIS MIAMI MILWAUKEE
## 833 530 2616 728
## MINNEAPOLIS NASHVILLE NEW ORLEANS-MOBILE OKLAHOMA CITY-TULSA
## 801 989 852 800
## OMAHA ORLANDO PHILADELPHIA PHOENIX
## 1017 1135 433 2263
## PITTSBURGH PORTLAND, OR RALEIGH-DURHAM RICHMOND
## 352 552 1126 1063
## RURAL ALABAMA RURAL ARKANSAS RURAL CALIFORNIA RURAL COLORADO
## 305 160 848 21
## RURAL FLORIDA RURAL GEORGIA RURAL IDAHO RURAL ILLINOIS
## 522 460 154 1195
## RURAL INDIANA RURAL IOWA RURAL KANSAS RURAL KENTUCKY
## 481 1060 179 225
## RURAL LOUISIANA RURAL MAINE RURAL MICHIGAN RURAL MINNESOTA
## 381 353 754 138
## RURAL MISSISSIPPI RURAL MISSOURI RURAL MONTANA RURAL NEBRASKA
## 354 640 354 110
## RURAL NEVADA RURAL NEW HAMPSHIRE RURAL NEW MEXICO RURAL NEW YORK
## 557 25 427 13
## RURAL NORTH CAROLINA RURAL NORTH DAKOTA RURAL OHIO RURAL OKLAHOMA
## 909 129 257 54
## RURAL OREGON RURAL PENNSYLVANIA RURAL SOUTH CAROLINA RURAL SOUTH DAKOTA
## 38 298 1295 153
## RURAL TENNESSEE RURAL TEXAS RURAL VERMONT RURAL VIRGINIA
## 423 1771 139 185
## RURAL WASHINGTON RURAL WEST VIRGINIA RURAL WISCONSIN RURAL WYOMING
## 330 265 1306 39
## SACRAMENTO SALT LAKE CITY SAN ANTONIO SAN DIEGO
## 981 320 2615 656
## SAN FRANCISCO SEATTLE ST. LOUIS SURBURBAN NY
## 871 903 1347 872
## SYRACUSE TAMPA URBAN NY WASHINGTON DC
## 294 3180 735 863Q1c
Create the data.frame that has a factor-type variable of
market whose reference level is “BUFFALO-ROCHESTER” using
the resulting data.frame from Q1b.
beer_markets$market <- relevel(beer_markets$market,
"BUFFALO-ROCHESTER")Q1d
Split the resulting data.frame of Q1c into training and testing data.frames such that approximately 67% of observations in the resulting data.frame of Q1c belong to the training data.frame and the rest observations belong to the testing data.frame.
set.seed(1234)
gp <- runif(nrow(beer_markets))
train <- filter(beer_markets, gp > .33) # training data
test <- filter(beer_markets, gp <= .33) # test dataQ1e
Consider the three linear regression models with the following three different formulas:
formula_1 <- log(price_per_floz) ~ market + container + brand + log(beer_floz)
formula_2 <- log(price_per_floz) ~ market + container + brand * log(beer_floz)
formula_3 <- log(price_per_floz) ~ market + container + brand * promo * log(beer_floz)Conduct exploratory data analysis regarding the model with
formula_3.
sum_train <- skimr::skim(
select(train,
price_per_floz, beer_floz,
container, brand, promo, market)
)
library(GGally)
ggpairs( select(train,
price_per_floz, beer_floz,
container, brand, promo) )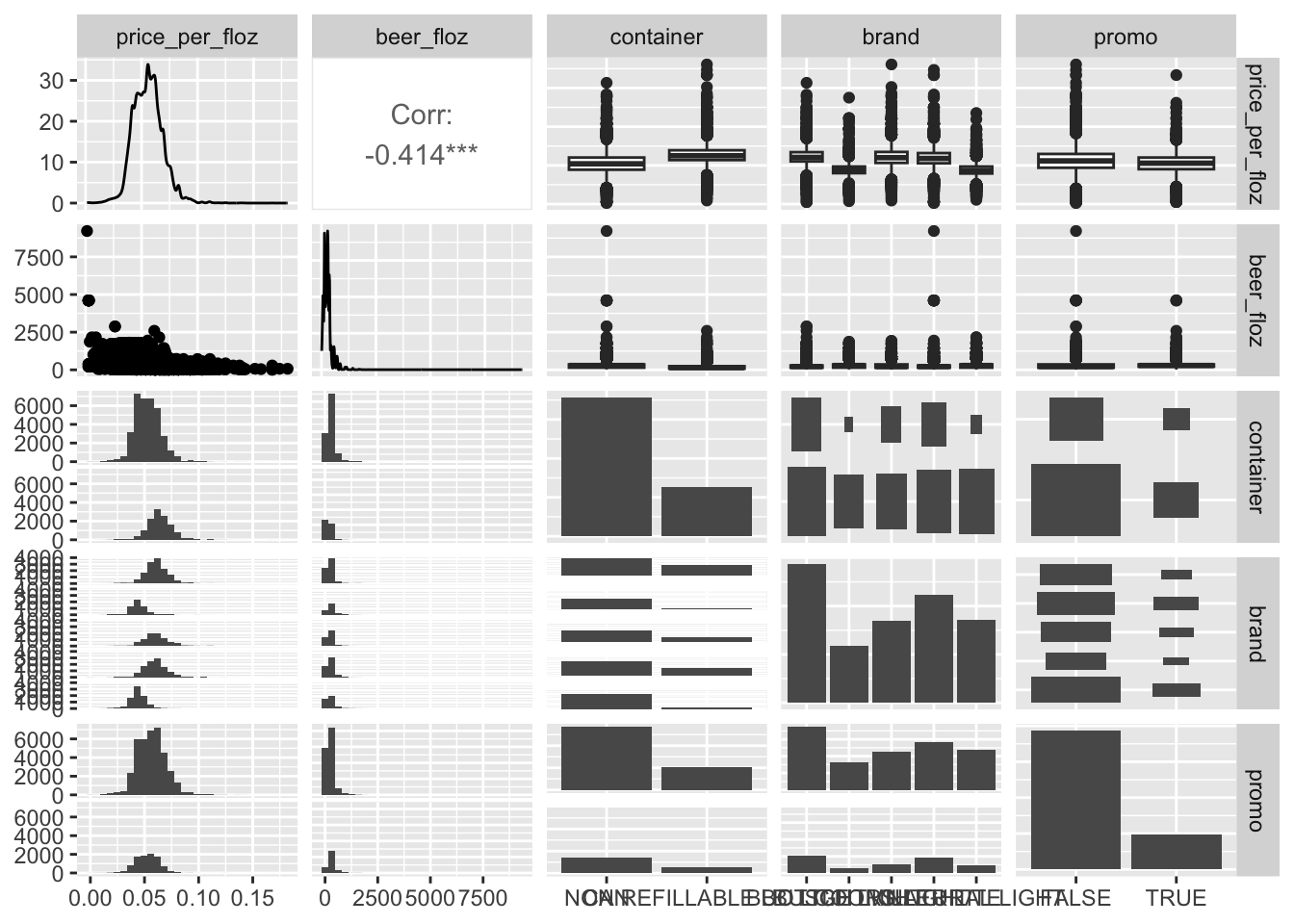 - More visualization should be considered.
- More visualization should be considered.
Q1f
Train the three linear regression models using the training data.frame from Q1d with the three different formulas,
formula_1,formula_2, andformula_3, provided in Q1e.What are the main goals of these linear regression models? Provide the summary of the result for each linear regression model.
Create the data.frame of all the beta estimates for all variables and their t-statistics and p-values from each model.
model_1 <- lm(formula_1, data = train)
model_2 <- lm(formula_2, data = train)
model_3 <- lm(formula_3, data = train)
# summary(model_1)
# summary(model_2)
# summary(model_3)
library(stargazer)
stargazer(model_1, model_2, model_3, type = 'html')| Dependent variable: | |||
| log(price_per_floz) | |||
| (1) | (2) | (3) | |
| marketALBANY | 0.039*** | 0.041*** | 0.036*** |
| (0.013) | (0.013) | (0.013) | |
| marketATLANTA | 0.091*** | 0.090*** | 0.088*** |
| (0.010) | (0.010) | (0.010) | |
| marketBALTIMORE | 0.104*** | 0.107*** | 0.099*** |
| (0.014) | (0.014) | (0.014) | |
| marketBIRMINGHAM | 0.129*** | 0.136*** | 0.134*** |
| (0.011) | (0.011) | (0.011) | |
| marketBOSTON | 0.125*** | 0.125*** | 0.123*** |
| (0.011) | (0.011) | (0.011) | |
| marketCHARLOTTE | 0.032*** | 0.028*** | 0.041*** |
| (0.010) | (0.010) | (0.010) | |
| marketCHICAGO | 0.003 | -0.003 | 0.006 |
| (0.010) | (0.010) | (0.010) | |
| marketCINCINNATI | 0.092*** | 0.087*** | 0.086*** |
| (0.010) | (0.010) | (0.010) | |
| marketCLEVELAND | 0.059*** | 0.054*** | 0.052*** |
| (0.011) | (0.010) | (0.010) | |
| marketCOLUMBUS | 0.082*** | 0.079*** | 0.081*** |
| (0.010) | (0.010) | (0.010) | |
| marketDALLAS | 0.214*** | 0.225*** | 0.230*** |
| (0.010) | (0.010) | (0.010) | |
| marketDENVER | 0.134*** | 0.132*** | 0.144*** |
| (0.011) | (0.011) | (0.011) | |
| marketDES MOINES | 0.143*** | 0.140*** | 0.135*** |
| (0.012) | (0.012) | (0.012) | |
| marketDETROIT | 0.094*** | 0.090*** | 0.095*** |
| (0.010) | (0.010) | (0.010) | |
| marketEXURBAN NY | 0.190*** | 0.186*** | 0.181*** |
| (0.014) | (0.014) | (0.014) | |
| marketGRAND RAPIDS | 0.092*** | 0.087*** | 0.088*** |
| (0.012) | (0.012) | (0.011) | |
| marketHARTFORD-NEW HAVEN | 0.149*** | 0.147*** | 0.146*** |
| (0.014) | (0.014) | (0.014) | |
| marketHOUSTON | 0.122*** | 0.119*** | 0.124*** |
| (0.010) | (0.010) | (0.010) | |
| marketINDIANAPOLIS | 0.051*** | 0.051*** | 0.054*** |
| (0.011) | (0.010) | (0.010) | |
| marketJACKSONVILLE | 0.125*** | 0.120*** | 0.124*** |
| (0.013) | (0.012) | (0.012) | |
| marketKANSAS CITY | 0.080*** | 0.076*** | 0.072*** |
| (0.012) | (0.012) | (0.012) | |
| marketLITTLE ROCK | 0.105*** | 0.102*** | 0.100*** |
| (0.013) | (0.013) | (0.013) | |
| marketLOS ANGELES | 0.037*** | 0.030*** | 0.041*** |
| (0.010) | (0.010) | (0.010) | |
| marketLOUISVILLE | 0.071*** | 0.066*** | 0.071*** |
| (0.011) | (0.011) | (0.011) | |
| marketMEMPHIS | 0.127*** | 0.125*** | 0.121*** |
| (0.013) | (0.012) | (0.012) | |
| marketMIAMI | 0.117*** | 0.115*** | 0.119*** |
| (0.010) | (0.010) | (0.009) | |
| marketMILWAUKEE | 0.037*** | 0.036*** | 0.040*** |
| (0.012) | (0.012) | (0.011) | |
| marketMINNEAPOLIS | 0.136*** | 0.138*** | 0.136*** |
| (0.011) | (0.011) | (0.011) | |
| marketNASHVILLE | 0.147*** | 0.146*** | 0.147*** |
| (0.011) | (0.011) | (0.011) | |
| marketNEW ORLEANS-MOBILE | 0.139*** | 0.128*** | 0.124*** |
| (0.011) | (0.011) | (0.011) | |
| marketOKLAHOMA CITY-TULSA | 0.152*** | 0.148*** | 0.142*** |
| (0.011) | (0.011) | (0.011) | |
| marketOMAHA | 0.125*** | 0.123*** | 0.127*** |
| (0.011) | (0.011) | (0.011) | |
| marketORLANDO | 0.105*** | 0.103*** | 0.108*** |
| (0.011) | (0.011) | (0.011) | |
| marketPHILADELPHIA | 0.117*** | 0.117*** | 0.106*** |
| (0.013) | (0.013) | (0.013) | |
| marketPHOENIX | 0.150*** | 0.152*** | 0.164*** |
| (0.010) | (0.010) | (0.010) | |
| marketPITTSBURGH | 0.099*** | 0.096*** | 0.091*** |
| (0.014) | (0.014) | (0.014) | |
| marketPORTLAND, OR | 0.122*** | 0.120*** | 0.124*** |
| (0.012) | (0.012) | (0.012) | |
| marketRALEIGH-DURHAM | 0.090*** | 0.091*** | 0.088*** |
| (0.011) | (0.011) | (0.011) | |
| marketRICHMOND | 0.048*** | 0.045*** | 0.041*** |
| (0.011) | (0.011) | (0.011) | |
| marketRURAL ALABAMA | 0.161*** | 0.160*** | 0.159*** |
| (0.014) | (0.014) | (0.014) | |
| marketRURAL ARKANSAS | 0.179*** | 0.181*** | 0.174*** |
| (0.019) | (0.019) | (0.018) | |
| marketRURAL CALIFORNIA | 0.049*** | 0.045*** | 0.049*** |
| (0.011) | (0.011) | (0.011) | |
| marketRURAL COLORADO | 0.197*** | 0.195*** | 0.204*** |
| (0.041) | (0.041) | (0.040) | |
| marketRURAL FLORIDA | 0.075*** | 0.065*** | 0.065*** |
| (0.013) | (0.013) | (0.012) | |
| marketRURAL GEORGIA | 0.144*** | 0.140*** | 0.136*** |
| (0.013) | (0.013) | (0.013) | |
| marketRURAL IDAHO | 0.156*** | 0.150*** | 0.152*** |
| (0.019) | (0.019) | (0.019) | |
| marketRURAL ILLINOIS | 0.020* | 0.019* | 0.019* |
| (0.011) | (0.011) | (0.010) | |
| marketRURAL INDIANA | 0.068*** | 0.070*** | 0.073*** |
| (0.013) | (0.012) | (0.012) | |
| marketRURAL IOWA | 0.072*** | 0.068*** | 0.066*** |
| (0.011) | (0.011) | (0.011) | |
| marketRURAL KANSAS | 0.136*** | 0.136*** | 0.130*** |
| (0.018) | (0.018) | (0.018) | |
| marketRURAL KENTUCKY | 0.164*** | 0.165*** | 0.162*** |
| (0.016) | (0.016) | (0.016) | |
| marketRURAL LOUISIANA | 0.082*** | 0.077*** | 0.069*** |
| (0.014) | (0.013) | (0.013) | |
| marketRURAL MAINE | 0.087*** | 0.085*** | 0.085*** |
| (0.014) | (0.014) | (0.014) | |
| marketRURAL MICHIGAN | 0.093*** | 0.091*** | 0.088*** |
| (0.012) | (0.011) | (0.011) | |
| marketRURAL MINNESOTA | 0.184*** | 0.187*** | 0.181*** |
| (0.019) | (0.019) | (0.019) | |
| marketRURAL MISSISSIPPI | 0.065*** | 0.060*** | 0.061*** |
| (0.014) | (0.014) | (0.014) | |
| marketRURAL MISSOURI | 0.119*** | 0.118*** | 0.113*** |
| (0.012) | (0.012) | (0.012) | |
| marketRURAL MONTANA | 0.132*** | 0.128*** | 0.138*** |
| (0.014) | (0.014) | (0.014) | |
| marketRURAL NEBRASKA | 0.137*** | 0.137*** | 0.136*** |
| (0.022) | (0.022) | (0.021) | |
| marketRURAL NEVADA | 0.058*** | 0.058*** | 0.059*** |
| (0.013) | (0.013) | (0.012) | |
| marketRURAL NEW HAMPSHIRE | 0.051 | 0.042 | 0.036 |
| (0.041) | (0.041) | (0.040) | |
| marketRURAL NEW MEXICO | 0.166*** | 0.161*** | 0.159*** |
| (0.013) | (0.013) | (0.013) | |
| marketRURAL NEW YORK | -0.009 | -0.008 | -0.020 |
| (0.057) | (0.057) | (0.057) | |
| marketRURAL NORTH CAROLINA | 0.021* | 0.051*** | 0.043*** |
| (0.011) | (0.011) | (0.011) | |
| marketRURAL NORTH DAKOTA | 0.216*** | 0.216*** | 0.216*** |
| (0.021) | (0.021) | (0.020) | |
| marketRURAL OHIO | 0.101*** | 0.099*** | 0.097*** |
| (0.016) | (0.016) | (0.016) | |
| marketRURAL OKLAHOMA | 0.157*** | 0.158*** | 0.148*** |
| (0.029) | (0.029) | (0.029) | |
| marketRURAL OREGON | 0.055 | 0.053 | 0.055 |
| (0.034) | (0.034) | (0.033) | |
| marketRURAL PENNSYLVANIA | 0.140*** | 0.140*** | 0.131*** |
| (0.015) | (0.015) | (0.015) | |
| marketRURAL SOUTH CAROLINA | 0.061*** | 0.061*** | 0.064*** |
| (0.010) | (0.010) | (0.010) | |
| marketRURAL SOUTH DAKOTA | 0.093*** | 0.090*** | 0.086*** |
| (0.018) | (0.018) | (0.018) | |
| marketRURAL TENNESSEE | 0.178*** | 0.178*** | 0.184*** |
| (0.013) | (0.013) | (0.013) | |
| marketRURAL TEXAS | 0.180*** | 0.179*** | 0.177*** |
| (0.010) | (0.010) | (0.010) | |
| marketRURAL VERMONT | 0.097*** | 0.085*** | 0.088*** |
| (0.019) | (0.019) | (0.019) | |
| marketRURAL VIRGINIA | 0.034* | 0.031* | 0.030* |
| (0.018) | (0.017) | (0.017) | |
| marketRURAL WASHINGTON | 0.105*** | 0.103*** | 0.120*** |
| (0.014) | (0.014) | (0.014) | |
| marketRURAL WEST VIRGINIA | -0.019 | -0.021 | -0.028* |
| (0.015) | (0.015) | (0.015) | |
| marketRURAL WISCONSIN | 0.053*** | 0.051*** | 0.053*** |
| (0.010) | (0.010) | (0.010) | |
| marketRURAL WYOMING | 0.115*** | 0.113*** | 0.111*** |
| (0.035) | (0.035) | (0.035) | |
| marketSACRAMENTO | 0.034*** | 0.034*** | 0.043*** |
| (0.011) | (0.011) | (0.011) | |
| marketSALT LAKE CITY | 0.122*** | 0.114*** | 0.112*** |
| (0.015) | (0.014) | (0.014) | |
| marketSAN ANTONIO | 0.147*** | 0.142*** | 0.140*** |
| (0.010) | (0.010) | (0.009) | |
| marketSAN DIEGO | 0.029** | 0.028** | 0.034*** |
| (0.012) | (0.012) | (0.012) | |
| marketSAN FRANCISCO | 0.078*** | 0.075*** | 0.084*** |
| (0.011) | (0.011) | (0.011) | |
| marketSEATTLE | 0.117*** | 0.108*** | 0.121*** |
| (0.011) | (0.011) | (0.011) | |
| marketST. LOUIS | 0.050*** | 0.047*** | 0.051*** |
| (0.010) | (0.010) | (0.010) | |
| marketSURBURBAN NY | 0.063*** | 0.060*** | 0.056*** |
| (0.011) | (0.011) | (0.011) | |
| marketSYRACUSE | -0.035** | -0.041*** | -0.047*** |
| (0.015) | (0.015) | (0.015) | |
| marketTAMPA | 0.113*** | 0.109*** | 0.112*** |
| (0.009) | (0.009) | (0.009) | |
| marketURBAN NY | 0.166*** | 0.165*** | 0.165*** |
| (0.011) | (0.011) | (0.011) | |
| marketWASHINGTON DC | 0.104*** | 0.099*** | 0.095*** |
| (0.011) | (0.011) | (0.011) | |
| containerNON REFILLABLE BOTTLE | 0.055*** | 0.054*** | 0.055*** |
| (0.002) | (0.002) | (0.002) | |
| brandBUSCH LIGHT | -0.259*** | -0.217*** | -0.180*** |
| (0.003) | (0.022) | (0.023) | |
| brandCOORS LIGHT | -0.002 | 0.010 | 0.024 |
| (0.002) | (0.019) | (0.020) | |
| brandMILLER LITE | -0.014*** | 0.101*** | 0.118*** |
| (0.002) | (0.017) | (0.018) | |
| brandNATURAL LIGHT | -0.317*** | -0.607*** | -0.544*** |
| (0.002) | (0.018) | (0.019) | |
| promo | -0.056 | ||
| (0.037) | |||
| log(beer_floz) | -0.141*** | -0.146*** | -0.141*** |
| (0.001) | (0.002) | (0.002) | |
| brandBUSCH LIGHT:promo | -0.219*** | ||
| (0.070) | |||
| brandCOORS LIGHT:promo | -0.154*** | ||
| (0.059) | |||
| brandMILLER LITE:promo | -0.168*** | ||
| (0.052) | |||
| brandNATURAL LIGHT:promo | -0.298*** | ||
| (0.051) | |||
| brandBUSCH LIGHT:log(beer_floz) | -0.008* | -0.015*** | |
| (0.004) | (0.004) | ||
| brandCOORS LIGHT:log(beer_floz) | -0.003 | -0.004 | |
| (0.003) | (0.004) | ||
| brandMILLER LITE:log(beer_floz) | -0.022*** | -0.024*** | |
| (0.003) | (0.003) | ||
| brandNATURAL LIGHT:log(beer_floz) | 0.054*** | 0.042*** | |
| (0.003) | (0.003) | ||
| promoTRUE:log(beer_floz) | 0.001 | ||
| (0.007) | |||
| brandBUSCH LIGHT:promoTRUE:log(beer_floz) | 0.041*** | ||
| (0.012) | |||
| brandCOORS LIGHT:promoTRUE:log(beer_floz) | 0.024** | ||
| (0.011) | |||
| brandMILLER LITE:promoTRUE:log(beer_floz) | 0.030*** | ||
| (0.009) | |||
| brandNATURAL LIGHT:promoTRUE:log(beer_floz) | 0.053*** | ||
| (0.009) | |||
| Constant | -2.183*** | -2.155*** | -2.172*** |
| (0.011) | (0.014) | (0.015) | |
| Observations | 48,384 | 48,384 | 48,384 |
| R2 | 0.546 | 0.551 | 0.559 |
| Adjusted R2 | 0.545 | 0.550 | 0.558 |
| Residual Std. Error | 0.170 (df = 48286) | 0.169 (df = 48282) | 0.168 (df = 48272) |
| F Statistic | 598.350*** (df = 97; 48286) | 586.770*** (df = 101; 48282) | 550.383*** (df = 111; 48272) |
| Note: | p<0.1; p<0.05; p<0.01 | ||
stargazer(model_1, model_2, model_3, type = 'html',
omit = c("market", "container", "Constant"))| Dependent variable: | |||
| log(price_per_floz) | |||
| (1) | (2) | (3) | |
| brandBUSCH LIGHT | -0.259*** | -0.217*** | -0.180*** |
| (0.003) | (0.022) | (0.023) | |
| brandCOORS LIGHT | -0.002 | 0.010 | 0.024 |
| (0.002) | (0.019) | (0.020) | |
| brandMILLER LITE | -0.014*** | 0.101*** | 0.118*** |
| (0.002) | (0.017) | (0.018) | |
| brandNATURAL LIGHT | -0.317*** | -0.607*** | -0.544*** |
| (0.002) | (0.018) | (0.019) | |
| promo | -0.056 | ||
| (0.037) | |||
| log(beer_floz) | -0.141*** | -0.146*** | -0.141*** |
| (0.001) | (0.002) | (0.002) | |
| brandBUSCH LIGHT:promo | -0.219*** | ||
| (0.070) | |||
| brandCOORS LIGHT:promo | -0.154*** | ||
| (0.059) | |||
| brandMILLER LITE:promo | -0.168*** | ||
| (0.052) | |||
| brandNATURAL LIGHT:promo | -0.298*** | ||
| (0.051) | |||
| brandBUSCH LIGHT:log(beer_floz) | -0.008* | -0.015*** | |
| (0.004) | (0.004) | ||
| brandCOORS LIGHT:log(beer_floz) | -0.003 | -0.004 | |
| (0.003) | (0.004) | ||
| brandMILLER LITE:log(beer_floz) | -0.022*** | -0.024*** | |
| (0.003) | (0.003) | ||
| brandNATURAL LIGHT:log(beer_floz) | 0.054*** | 0.042*** | |
| (0.003) | (0.003) | ||
| promoTRUE:log(beer_floz) | 0.001 | ||
| (0.007) | |||
| brandBUSCH LIGHT:promoTRUE:log(beer_floz) | 0.041*** | ||
| (0.012) | |||
| brandCOORS LIGHT:promoTRUE:log(beer_floz) | 0.024** | ||
| (0.011) | |||
| brandMILLER LITE:promoTRUE:log(beer_floz) | 0.030*** | ||
| (0.009) | |||
| brandNATURAL LIGHT:promoTRUE:log(beer_floz) | 0.053*** | ||
| (0.009) | |||
| Observations | 48,384 | 48,384 | 48,384 |
| R2 | 0.546 | 0.551 | 0.559 |
| Adjusted R2 | 0.545 | 0.550 | 0.558 |
| Residual Std. Error | 0.170 (df = 48286) | 0.169 (df = 48282) | 0.168 (df = 48272) |
| F Statistic | 598.350*** (df = 97; 48286) | 586.770*** (df = 101; 48282) | 550.383*** (df = 111; 48272) |
| Note: | p<0.1; p<0.05; p<0.01 | ||
b1 <- coef(model_1)
b2 <- coef(model_2)
b3 <- coef(model_3)
library(broom)
df_b1 <- tidy(model_1)
df_b2 <- tidy(model_2)
df_b3 <- tidy(model_3)- The goal of these linear regression is to answer the following questions:
- How are the explanatory variables—sales volume, promotion, and brand characteristics (e.g, consumer loyalty, beer taste)—related with the beer price?
- Given the linear relationship between the outcome and the explanatory variables, what are the predicted beer prices for unseen data?
- Intuition behind the model:
- I choose the pricing model. The beer industry is close to oligopoly, which means that each beer company has enough market power to set the price level above its competitive level of price.
- Each beer company sets the price of a brand’s beer based on the degree of consumers’ loyalty, sales volume, promotion, container type, and market characteristics (as well as various consumer characteristics).
Q1g
Interpret the beta estimates of the following variables from the
model with formula_3. - (1) marketALBANY - (2)
marketEXURBAN NY - (3) marketRURAL NEW YORK -
(4) marketSURBURBAN NY - (5) marketSYRACUSE -
(6) marketURBAN NY
q1g_df_b3 <- df_b3 %>%
filter(str_detect(term, "marketALBANY") |
str_detect(term, "marketEXURBAN NY") |
str_detect(term, "marketRURAL NEW YORK") |
str_detect(term, "marketSURBURBAN NY") |
str_detect(term, "marketSYRACUSE") |
str_detect(term, "marketURBAN NY") ) %>%
mutate(sinificance = ifelse(p.value <= .1, T, F)) %>%
select(sinificance, everything())
# beta for marketRURAL NEW YORK is not statistically significantb3['marketALBANY'] # ***## marketALBANY
## 0.0358602exp(b3['marketALBANY']) # 1.036511 ## marketALBANY
## 1.036511- All else being equal, being in
ALBANYrelative to being inBUFFALO-ROCHESTERis associated with an increase inprice_per_flozby 3.65%.
- All else being equal, being in
b3['marketEXURBAN NY'] # ***## marketEXURBAN NY
## 0.1808736exp(b3['marketEXURBAN NY'])## marketEXURBAN NY
## 1.198264- All else being equal, being in
EXURBAN NYrelative to being inBUFFALO-ROCHESTERis associated with an increase inprice_per_flozby 19.83%.
- All else being equal, being in
b3['marketRURAL NEW YORK'] # there is no star## marketRURAL NEW YORK
## -0.02045906- We cannot reject the null hypothesis that the beta coefficient for
the variable
marketRURAL NEW YORKis zero.
- We cannot reject the null hypothesis that the beta coefficient for
the variable
b3['marketSURBURBAN NY'] # ***## marketSURBURBAN NY
## 0.05639214exp(b3['marketSURBURBAN NY'])## marketSURBURBAN NY
## 1.058012- All else being equal, being in
SURBURBAN NYrelative to being inBUFFALO-ROCHESTERis associated with an increase inprice_per_flozby 5.80%
- All else being equal, being in
b3['marketSYRACUSE'] # ***## marketSYRACUSE
## -0.04721861exp(b3['marketSYRACUSE'])## marketSYRACUSE
## 0.95387881 - exp(b3['marketSYRACUSE'])## marketSYRACUSE
## 0.04612116- All else being equal, being in
SYRACUSErelative to being inBUFFALO-ROCHESTERis associated with a decrease inprice_per_flozby 4.61%.
- All else being equal, being in
b3['marketURBAN NY'] # ***## marketURBAN NY
## 0.1652982exp(b3['marketURBAN NY'])## marketURBAN NY
## 1.179745- All else being equal, being in
URBAN NYrelative to being inBUFFALO-ROCHESTERis associated with an increase inprice_per_flozby 17.97%.
- All else being equal, being in
Q1h
Across the three models in Q1f, how is the percentage change in the price of beer sensitive to the percentage change in the volume of beer purchases for each brand?
In the model with
formula_3, how does such sensitivity vary bypromo?
q1h_df_b1 <- tidy(model_1) %>%
filter( !str_detect(term, "market"),
!str_detect(term, "container") ) %>%
mutate(sinificance = ifelse(p.value <= .1, T, F)) %>%
select(sinificance, everything())
q1h_df_b2 <- tidy(model_2) %>%
filter( !str_detect(term, "market"),
!str_detect(term, "container") ) %>%
mutate(sinificance = ifelse(p.value <= .1, T, F)) %>%
select(sinificance, everything())
q1h_df_b3 <- tidy(model_3) %>%
filter( !str_detect(term, "market"),
!str_detect(term, "container") ) %>%
mutate(sinificance = ifelse(p.value <= .1, T, F)) %>%
select(sinificance, everything())# Model 1
q1h_df_b1sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | statistic <dbl> | p.value <dbl> |
|---|---|---|---|---|---|
| TRUE | (Intercept) | -2.183064802 | 0.010976341 | -198.8882125 | 0.000000e+00 |
| TRUE | brandBUSCH LIGHT | -0.259468025 | 0.002827814 | -91.7556824 | 0.000000e+00 |
| FALSE | brandCOORS LIGHT | -0.002350587 | 0.002418288 | -0.9720043 | 3.310533e-01 |
| TRUE | brandMILLER LITE | -0.013929414 | 0.002237716 | -6.2248358 | 4.860134e-10 |
| TRUE | brandNATURAL LIGHT | -0.316768792 | 0.002498843 | -126.7661949 | 0.000000e+00 |
| TRUE | log(beer_floz) | -0.140895793 | 0.001179720 | -119.4315968 | 0.000000e+00 |
(sensitivity1_ALL <- b1['log(beer_floz)'])## log(beer_floz)
## -0.1408958- All else being equal, 1% increase in
beer_flozis associated with a decrease inprice_per_flozby 0.141%.
# Model 2
q1h_df_b2sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|---|
| TRUE | (Intercept) | -2.154586555 | 0.014455071 | |
| TRUE | brandBUSCH LIGHT | -0.216924466 | 0.022128719 | |
| FALSE | brandCOORS LIGHT | 0.010419276 | 0.018600442 | |
| TRUE | brandMILLER LITE | 0.101462362 | 0.016775190 | |
| TRUE | brandNATURAL LIGHT | -0.606670843 | 0.017559934 | |
| TRUE | log(beer_floz) | -0.145758400 | 0.002145872 | |
| TRUE | brandBUSCH LIGHT:log(beer_floz) | -0.007589650 | 0.004006932 | |
| FALSE | brandCOORS LIGHT:log(beer_floz) | -0.002500272 | 0.003459002 | |
| TRUE | brandMILLER LITE:log(beer_floz) | -0.021553032 | 0.003116647 | |
| TRUE | brandNATURAL LIGHT:log(beer_floz) | 0.053731615 | 0.003238282 |
## BUD LIGHT
(sensitivity2_BUD <- b2['log(beer_floz)'])## log(beer_floz)
## -0.1457584- All else being equal, an increase in
BUD LIGHTbeer_flozby 1% is associated with a decrease in itsprice_per_flozby 0.146%.
q1h_df_b2sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|---|
| TRUE | (Intercept) | -2.154586555 | 0.014455071 | |
| TRUE | brandBUSCH LIGHT | -0.216924466 | 0.022128719 | |
| FALSE | brandCOORS LIGHT | 0.010419276 | 0.018600442 | |
| TRUE | brandMILLER LITE | 0.101462362 | 0.016775190 | |
| TRUE | brandNATURAL LIGHT | -0.606670843 | 0.017559934 | |
| TRUE | log(beer_floz) | -0.145758400 | 0.002145872 | |
| TRUE | brandBUSCH LIGHT:log(beer_floz) | -0.007589650 | 0.004006932 | |
| FALSE | brandCOORS LIGHT:log(beer_floz) | -0.002500272 | 0.003459002 | |
| TRUE | brandMILLER LITE:log(beer_floz) | -0.021553032 | 0.003116647 | |
| TRUE | brandNATURAL LIGHT:log(beer_floz) | 0.053731615 | 0.003238282 |
## BUSCH LIGHT
(sensitivity2_BUSCH <-
b2['log(beer_floz)'] + b2['brandBUSCH LIGHT:log(beer_floz)'])## log(beer_floz)
## -0.1533481- All else being equal, an increase in
BUSCH LIGHTbeer_flozby 1% is associated with a decrease in itsprice_per_flozby 0.153%.
q1h_df_b2sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|---|
| TRUE | (Intercept) | -2.154586555 | 0.014455071 | |
| TRUE | brandBUSCH LIGHT | -0.216924466 | 0.022128719 | |
| FALSE | brandCOORS LIGHT | 0.010419276 | 0.018600442 | |
| TRUE | brandMILLER LITE | 0.101462362 | 0.016775190 | |
| TRUE | brandNATURAL LIGHT | -0.606670843 | 0.017559934 | |
| TRUE | log(beer_floz) | -0.145758400 | 0.002145872 | |
| TRUE | brandBUSCH LIGHT:log(beer_floz) | -0.007589650 | 0.004006932 | |
| FALSE | brandCOORS LIGHT:log(beer_floz) | -0.002500272 | 0.003459002 | |
| TRUE | brandMILLER LITE:log(beer_floz) | -0.021553032 | 0.003116647 | |
| TRUE | brandNATURAL LIGHT:log(beer_floz) | 0.053731615 | 0.003238282 |
## COORS LIGHT
(sensitivity2_COORS <- b2['log(beer_floz)'])## log(beer_floz)
## -0.1457584All else being equal, an increase in
COORS LIGHTbeer_flozby 1% is associated with a decrease in itsprice_per_flozby 0.146%.cf) There are no stars (or dots) next to
b2['brandCOORS LIGHT:log(beer_floz)'], meaning that it is not statistically significant.So we cannot reject the null hypotheses that the beta coefficient for the variable,
brandCOORS LIGHT:log(beer_floz)is zero.
q1h_df_b2sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|---|
| TRUE | (Intercept) | -2.154586555 | 0.014455071 | |
| TRUE | brandBUSCH LIGHT | -0.216924466 | 0.022128719 | |
| FALSE | brandCOORS LIGHT | 0.010419276 | 0.018600442 | |
| TRUE | brandMILLER LITE | 0.101462362 | 0.016775190 | |
| TRUE | brandNATURAL LIGHT | -0.606670843 | 0.017559934 | |
| TRUE | log(beer_floz) | -0.145758400 | 0.002145872 | |
| TRUE | brandBUSCH LIGHT:log(beer_floz) | -0.007589650 | 0.004006932 | |
| FALSE | brandCOORS LIGHT:log(beer_floz) | -0.002500272 | 0.003459002 | |
| TRUE | brandMILLER LITE:log(beer_floz) | -0.021553032 | 0.003116647 | |
| TRUE | brandNATURAL LIGHT:log(beer_floz) | 0.053731615 | 0.003238282 |
## MILLER LITE
(sensitivity2_MILLER <-
b2['log(beer_floz)'] + b2['brandMILLER LITE:log(beer_floz)'])## log(beer_floz)
## -0.1673114- All else being equal, an increase in
MILLER LITEbeer_flozby 1% is associated with a decrease in itsprice_per_flozby 0.167%.
q1h_df_b2sinificance <lgl> | term <chr> | estimate <dbl> | std.error <dbl> | |
|---|---|---|---|---|
| TRUE | (Intercept) | -2.154586555 | 0.014455071 | |
| TRUE | brandBUSCH LIGHT | -0.216924466 | 0.022128719 | |
| FALSE | brandCOORS LIGHT | 0.010419276 | 0.018600442 | |
| TRUE | brandMILLER LITE | 0.101462362 | 0.016775190 | |
| TRUE | brandNATURAL LIGHT | -0.606670843 | 0.017559934 | |
| TRUE | log(beer_floz) | -0.145758400 | 0.002145872 | |
| TRUE | brandBUSCH LIGHT:log(beer_floz) | -0.007589650 | 0.004006932 | |
| FALSE | brandCOORS LIGHT:log(beer_floz) | -0.002500272 | 0.003459002 | |
| TRUE | brandMILLER LITE:log(beer_floz) | -0.021553032 | 0.003116647 | |
| TRUE | brandNATURAL LIGHT:log(beer_floz) | 0.053731615 | 0.003238282 |
## NATURAL LIGHT
(sensitivity2_NATURAL <-
b2['log(beer_floz)'] + b2['brandNATURAL LIGHT:log(beer_floz)'])## log(beer_floz)
## -0.09202679- All else being equal, an increase in
NATURAL LIGHTbeer_flozby 1% is associated with a decrease in itsprice_per_flozby 0.092%.
# Model 3
q1h_df_b3sinificance <lgl> | term <chr> | estimate <dbl> | |
|---|---|---|---|
| TRUE | (Intercept) | -2.171652708 | |
| TRUE | brandBUSCH LIGHT | -0.180401422 | |
| FALSE | brandCOORS LIGHT | 0.024332791 | |
| TRUE | brandMILLER LITE | 0.117647580 | |
| TRUE | brandNATURAL LIGHT | -0.544211671 | |
| FALSE | promoTRUE | -0.056354727 | |
| TRUE | log(beer_floz) | -0.141068187 | |
| TRUE | brandBUSCH LIGHT:promoTRUE | -0.219213848 | |
| TRUE | brandCOORS LIGHT:promoTRUE | -0.154348835 | |
| TRUE | brandMILLER LITE:promoTRUE | -0.167569963 |
## BUD LIGHT
(sensitivity3_BUD_NOpromo <- b3['log(beer_floz)'])## log(beer_floz)
## -0.1410682(sensitivity3_BUD_promo <- b3['log(beer_floz)'])## log(beer_floz)
## -0.1410682All else being equal, an increase in
BUD LIGHTsales by 1% with or withoutpromois associated with a decrease in itsprice_per_flozby 0.141%cf)
b3['promoTRUE:log(beer_floz)']is not statistically significant.
q1h_df_b3sinificance <lgl> | term <chr> | estimate <dbl> | |
|---|---|---|---|
| TRUE | (Intercept) | -2.171652708 | |
| TRUE | brandBUSCH LIGHT | -0.180401422 | |
| FALSE | brandCOORS LIGHT | 0.024332791 | |
| TRUE | brandMILLER LITE | 0.117647580 | |
| TRUE | brandNATURAL LIGHT | -0.544211671 | |
| FALSE | promoTRUE | -0.056354727 | |
| TRUE | log(beer_floz) | -0.141068187 | |
| TRUE | brandBUSCH LIGHT:promoTRUE | -0.219213848 | |
| TRUE | brandCOORS LIGHT:promoTRUE | -0.154348835 | |
| TRUE | brandMILLER LITE:promoTRUE | -0.167569963 |
## BUSCH LIGHT
(sensitivity3_BUSCH_NOpromo <-
b3['log(beer_floz)'] + b3['brandBUSCH LIGHT:log(beer_floz)'])## log(beer_floz)
## -0.1561043(sensitivity3_BUSCH_promo <-
b3['log(beer_floz)'] + b3['brandBUSCH LIGHT:log(beer_floz)'] +
b3['brandBUSCH LIGHT:promoTRUE:log(beer_floz)'])## log(beer_floz)
## -0.1152271All else being equal, an increase in
BUSCH LIGHTsales by 1% withoutpromois associated with a decrease in itsprice_per_flozby 0.156%.All else being equal, an increase in
BUSCH LIGHTsales by 1% withpromois associated with a decrease in itsprice_per_flozby 0.115%.
q1h_df_b3sinificance <lgl> | term <chr> | estimate <dbl> | |
|---|---|---|---|
| TRUE | (Intercept) | -2.171652708 | |
| TRUE | brandBUSCH LIGHT | -0.180401422 | |
| FALSE | brandCOORS LIGHT | 0.024332791 | |
| TRUE | brandMILLER LITE | 0.117647580 | |
| TRUE | brandNATURAL LIGHT | -0.544211671 | |
| FALSE | promoTRUE | -0.056354727 | |
| TRUE | log(beer_floz) | -0.141068187 | |
| TRUE | brandBUSCH LIGHT:promoTRUE | -0.219213848 | |
| TRUE | brandCOORS LIGHT:promoTRUE | -0.154348835 | |
| TRUE | brandMILLER LITE:promoTRUE | -0.167569963 |
## COORS LIGHT
(sensitivity3_COORS_NOpromo <- b3['log(beer_floz)'])## log(beer_floz)
## -0.1410682(sensitivity3_COORS_promo <-
b3['log(beer_floz)']+ b3['brandCOORS LIGHT:promoTRUE:log(beer_floz)'])## log(beer_floz)
## -0.1173336All else being equal, an increase in
COORS LIGHTsales by 1% withoutpromois associated with a decrease in itsprice_per_flozby 0.141%.All else being equal, an increase in
COORS LIGHTsales by 1% withpromois associated with a decrease in itsprice_per_flozby 0.117%.
q1h_df_b3sinificance <lgl> | term <chr> | estimate <dbl> | |
|---|---|---|---|
| TRUE | (Intercept) | -2.171652708 | |
| TRUE | brandBUSCH LIGHT | -0.180401422 | |
| FALSE | brandCOORS LIGHT | 0.024332791 | |
| TRUE | brandMILLER LITE | 0.117647580 | |
| TRUE | brandNATURAL LIGHT | -0.544211671 | |
| FALSE | promoTRUE | -0.056354727 | |
| TRUE | log(beer_floz) | -0.141068187 | |
| TRUE | brandBUSCH LIGHT:promoTRUE | -0.219213848 | |
| TRUE | brandCOORS LIGHT:promoTRUE | -0.154348835 | |
| TRUE | brandMILLER LITE:promoTRUE | -0.167569963 |
## MILLER LITE
(sensitivity3_MILLER_NOpromo <-
b3['log(beer_floz)'] + b3['brandMILLER LITE:log(beer_floz)'])## log(beer_floz)
## -0.1654951(sensitivity3_MILLER_promo <-
b3['log(beer_floz)'] + b3['brandMILLER LITE:log(beer_floz)'] +
b3['brandMILLER LITE:promoTRUE:log(beer_floz)'])## log(beer_floz)
## -0.1352884All else being equal, an increase in
MILLER LITEsales by 1% withoutpromois associated with a decrease in itsprice_per_flozby 0.165%.All else being equal, an increase in
MILLER LITEsales by 1% withpromois associated with a decrease in itsprice_per_flozby 0.135%.
q1h_df_b3sinificance <lgl> | term <chr> | estimate <dbl> | |
|---|---|---|---|
| TRUE | (Intercept) | -2.171652708 | |
| TRUE | brandBUSCH LIGHT | -0.180401422 | |
| FALSE | brandCOORS LIGHT | 0.024332791 | |
| TRUE | brandMILLER LITE | 0.117647580 | |
| TRUE | brandNATURAL LIGHT | -0.544211671 | |
| FALSE | promoTRUE | -0.056354727 | |
| TRUE | log(beer_floz) | -0.141068187 | |
| TRUE | brandBUSCH LIGHT:promoTRUE | -0.219213848 | |
| TRUE | brandCOORS LIGHT:promoTRUE | -0.154348835 | |
| TRUE | brandMILLER LITE:promoTRUE | -0.167569963 |
## NATURAL LIGHT
(sensitivity3_NATURAL_NOpromo <-
b3['log(beer_floz)'] + b3['brandNATURAL LIGHT:log(beer_floz)'])## log(beer_floz)
## -0.09924425(sensitivity3_NATURAL_promo <-
b3['log(beer_floz)'] + b3['brandNATURAL LIGHT:log(beer_floz)'] +
b3['brandNATURAL LIGHT:promoTRUE:log(beer_floz)'])## log(beer_floz)
## -0.04637121All else being equal, an increase in
NATURAL LIGHTsales by 1% withoutpromois associated with a decrease in itsprice_per_flozby 0.099%.All else being equal, an increase in
NATURAL LIGHTsales by 1% withpromois associated with a decrease in itsprice_per_flozby 0.046%.
# all elasticities in one data.frame:
sensitivity <- data.frame(
brand = c('BUD LIGHT', 'BUSCH LIGHT', 'COORS LIGHT', 'MILLER LITE', 'NATURAL LIGHT'),
model1 = round(sensitivity1_ALL, digits = 4),
model2 = round(c(sensitivity2_BUD, sensitivity2_BUSCH, sensitivity2_COORS, sensitivity2_MILLER, sensitivity2_NATURAL), digits = 4),
model3_NOpromo = round(c(sensitivity3_BUD_NOpromo, sensitivity3_BUSCH_NOpromo, sensitivity3_COORS_NOpromo, sensitivity3_MILLER_NOpromo, sensitivity3_NATURAL_NOpromo), digits = 4),
model3_promo = round(c(sensitivity3_BUD_promo, sensitivity3_BUSCH_promo, sensitivity3_COORS_promo, sensitivity3_MILLER_promo, sensitivity3_NATURAL_promo), digits = 4)
)
sensitivitybrand <chr> | model1 <dbl> | model2 <dbl> | model3_NOpromo <dbl> | model3_promo <dbl> |
|---|---|---|---|---|
| BUD LIGHT | -0.1409 | -0.1458 | -0.1411 | -0.1411 |
| BUSCH LIGHT | -0.1409 | -0.1533 | -0.1561 | -0.1152 |
| COORS LIGHT | -0.1409 | -0.1458 | -0.1411 | -0.1173 |
| MILLER LITE | -0.1409 | -0.1673 | -0.1655 | -0.1353 |
| NATURAL LIGHT | -0.1409 | -0.0920 | -0.0992 | -0.0464 |
In
model_1, the volume sensitivity to changes in price does not vary bybrand.In
model_2, the volume sensitivity to changes in price varies bybrand.MILLER LITEis the most sensitive one.NATURAL LIGHTis the least sensitive one.BUD LIGHTandCOORS LIGHThave the same sensitivity.
In
model_3, the brand-specific volume sensitivity to changes in price can vary bypromo.- For all beer brands except for
BUD LIGHT,promo == TRUEmade their demands less sensitive!
- For all beer brands except for
Q1i
- For each model in Q1f, draw a residual plot.
- On average, are the prediction correct? Are there systematic errors?
- Which model do you prefer most and why?
test <- test %>%
mutate( pred_1 = predict(model_1, newdata = test),
pred_2 = predict(model_2, newdata = test),
pred_3 = predict(model_3, newdata = test) )
# residual plot
p1 <- ggplot(data = test, aes(x = pred_1,
y = log(price_per_floz) - pred_1 )) +
geom_point(color = 'grey60', alpha = .1) +
geom_smooth(color = 'blue') +
geom_hline(aes(yintercept = 0), color = 'red') + # y = 0
theme_minimal()
p1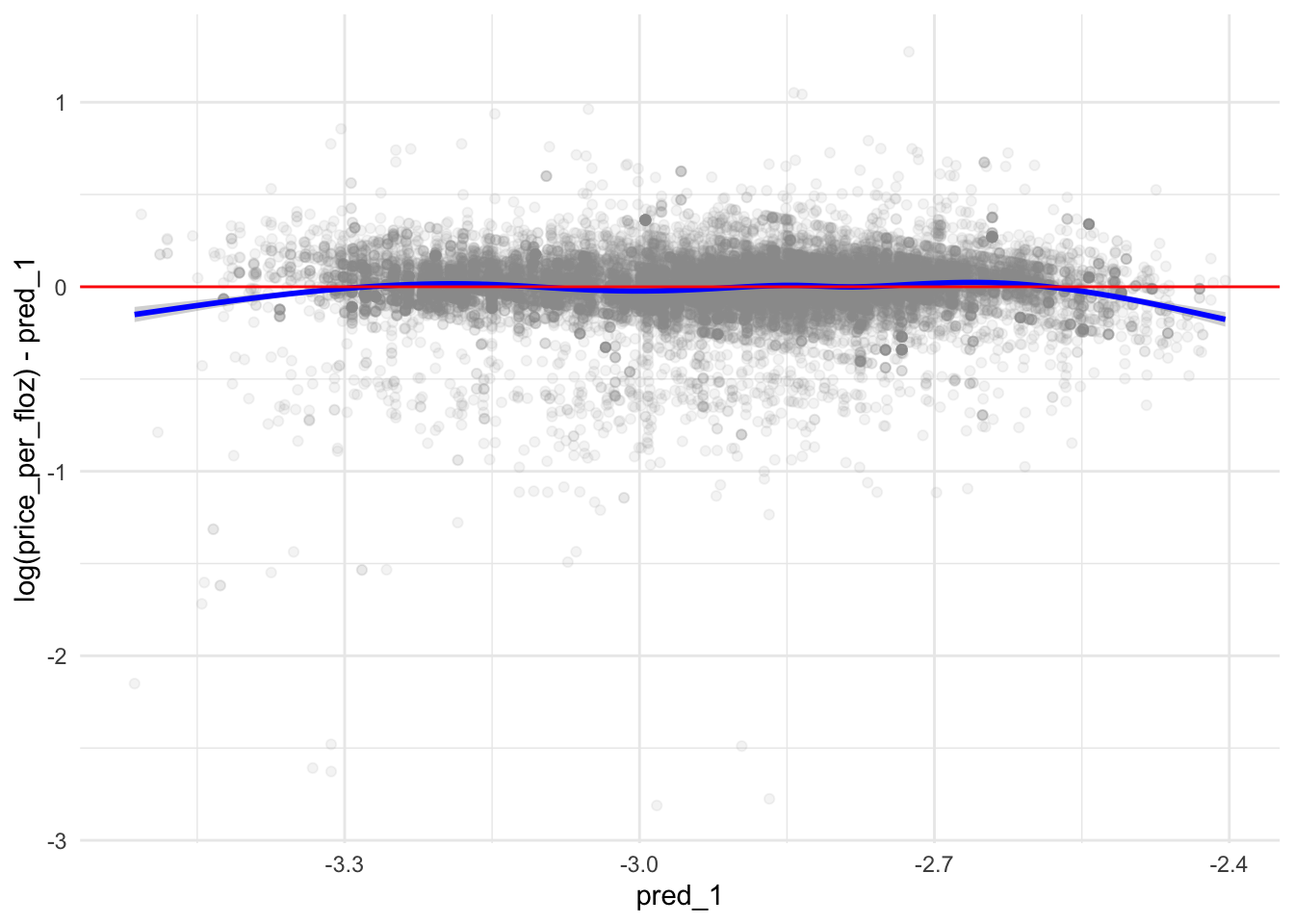
p2 <- ggplot(data = test, aes(x = pred_2,
y = log(price_per_floz) - pred_2 )) +
geom_point(color = 'grey60', alpha = .1) +
geom_smooth(color = 'blue') +
geom_hline(aes(yintercept = 0), color = 'red') + # y = 0
theme_minimal()
p2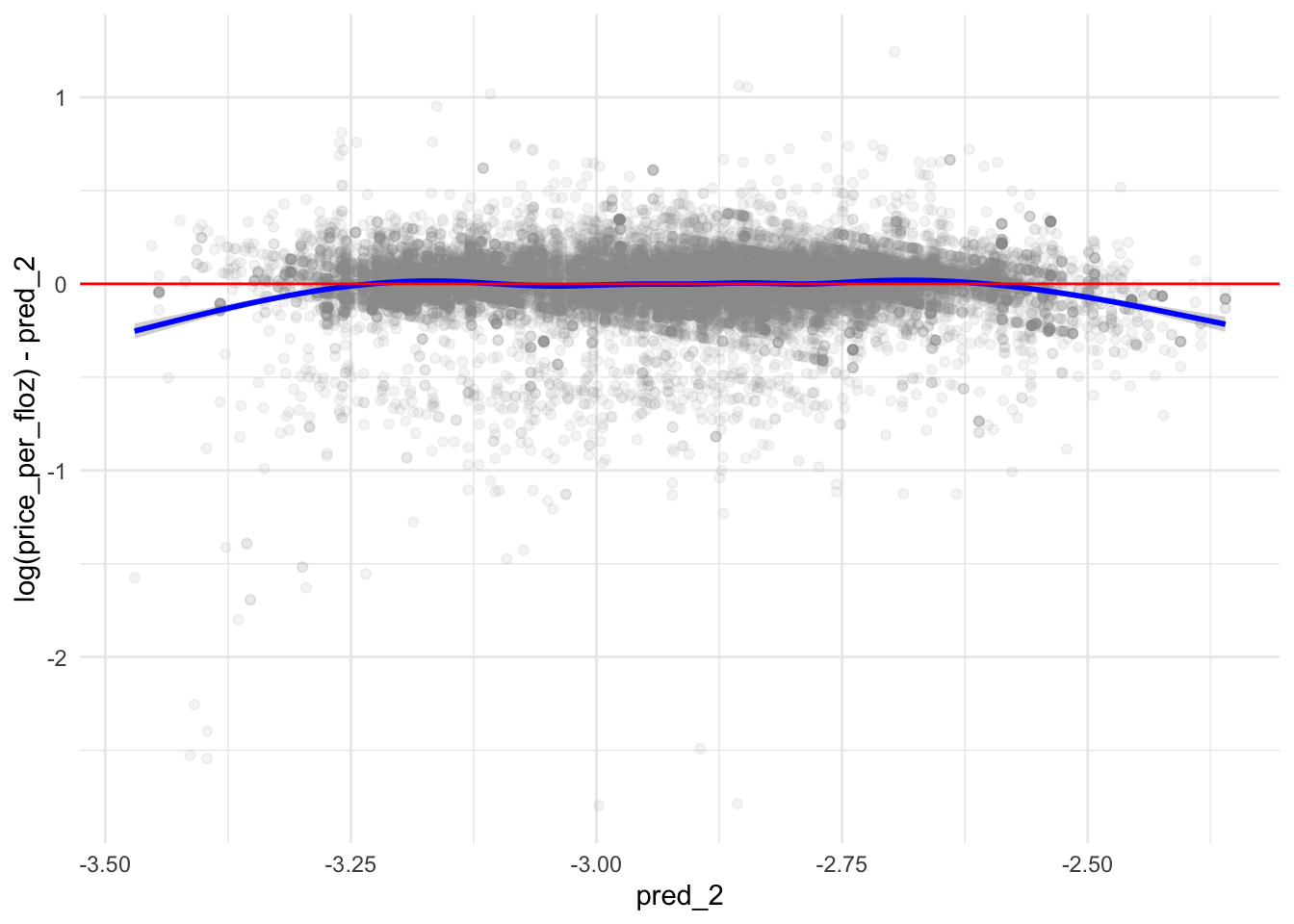
p3 <- ggplot(data = test, aes(x = pred_3,
y = log(price_per_floz) - pred_3 )) +
geom_point(color = 'grey60', alpha = .1) +
geom_smooth(color = 'blue') +
geom_hline(aes(yintercept = 0), color = 'red') + # y = 0
theme_minimal()
p3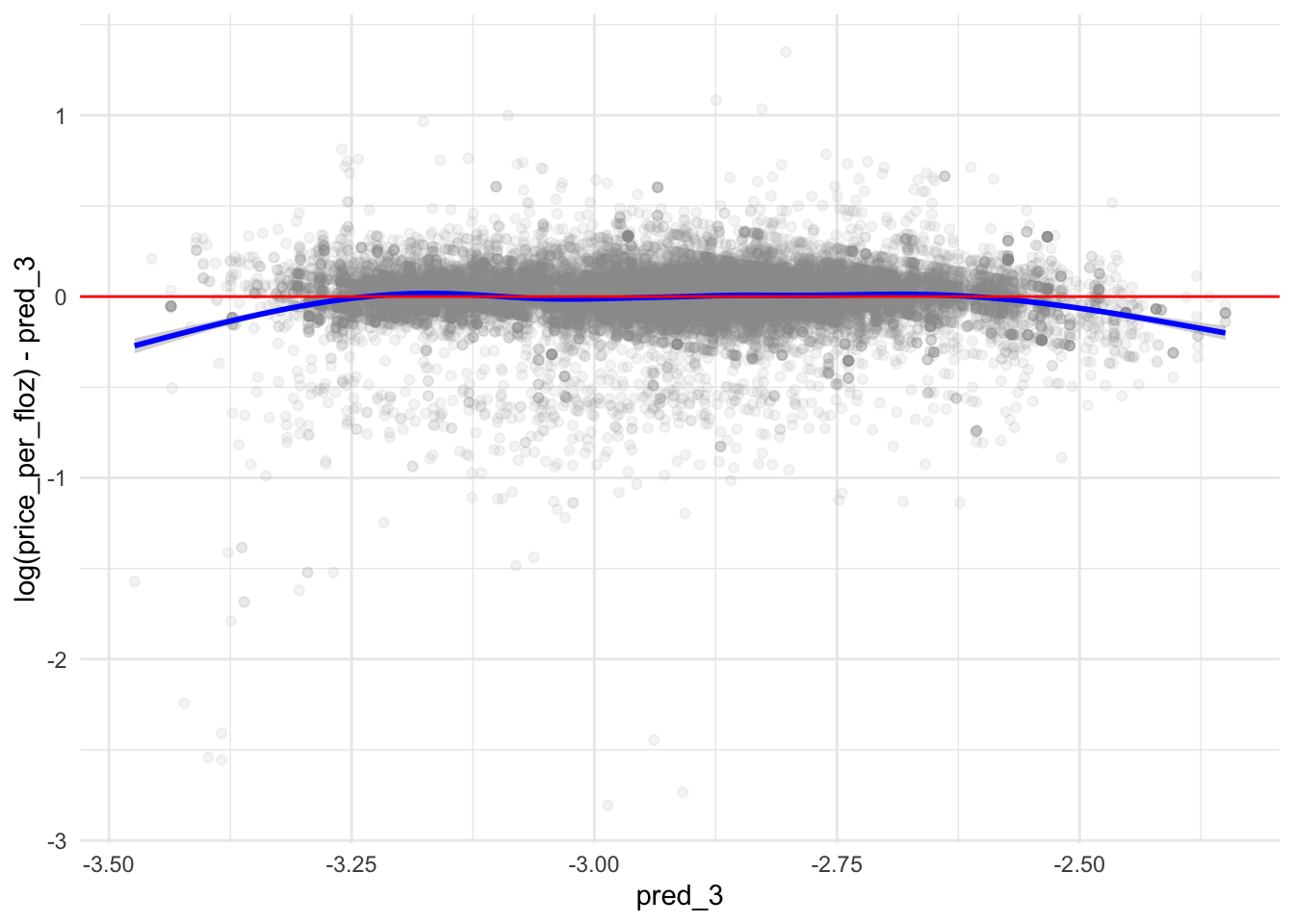 - When answering the question—Which model do you prefer most and why?—,
we can consider intuition behind formulas across models and the
significance of beta estimates.
- When answering the question—Which model do you prefer most and why?—,
we can consider intuition behind formulas across models and the
significance of beta estimates.
- Which model do you prefer most and why?
- I prefer model 3.
- The beta estimates for promo-related interaction terms except for
BUD LIGHTare statistically significant. - Intuitively, promotion affects purchasing decision of consumers who are sufficiently sensitive to changes in beer volumes.
- So,
promois likely to be a relevant variable to explain the variation of the beer price.