+ - 0:00:00
Notes for current slide
Notes for next slide

Lecture 23

DANL 200: Introduction to Data Analytics

Byeong-Hak Choe

November 22, 2022

1 / 37

Modeling Methods - Linear Regression

2 / 37

Linear Regression

Example

  • Suppose we also want to estimate how gender will affect personal income.
  • Linear regression assumes that ...
    • The outcome PINCP[i] is linearly related to each of the inputs AGEP[i] and SEX[i]:

PINCP[i]=f(AGEP[i], SEX[i])+e[i]=b0+b1*AGEP[i]+b2*SEX[i]+e[i]

  • A variable on the left-hand side is called an outcome variable or a dependent variable.
  • Variables on the right-hand side are called explanatory variables, independent variables, or input variables.
  • Coefficients b[1],...,b[P] on the right-hand side are called beta coefficients.
3 / 37

Linear Regression

Goals of Linear Regression

  • The goals of linear regression are ...

    1. Find the estimated values of b1 and b2: ^b1 and ^b2.

    2. Make a prediction on PINCP[i] for each person i: ^PINCP[i].

^PINCP[i]=^b0+^b1*AGEP[i]+^b2*SEX[i]

  • We will use the hat notation (ˆ ) to distinguish estimated beta coefficients and predicted outcomes from true values of beta coefficients and true values of outcome variables, respectively.
4 / 37

Linear Regression

Assumptions on Linear Regression

  • Assumptions on the linear regression model are that ...

    • The outcome variable is a linear combination of the explanatory variables.

    • Errors have a mean value of 0.

    • Errors are uncorrelated with explanatory variables.

5 / 37

Linear Regression

Beta estimates

  • Linear regression finds the beta coefficients (b[0],...,b[P]) such that ...

    – The linear function f(x[i, ]) is as near as possible to y[i] for all (x[i, ], y[i]) pairs in the data.

  • In other words, the estimator for the beta coefficients is chosen to minimize the sum of squares of the residual errors (SSR):

    • Residual_Error[i] = y[i] - ˆy[i].

    • SSR=Residual_Error[1]2+⋯+Residual_Error[N]2.

6 / 37

Linear Regression

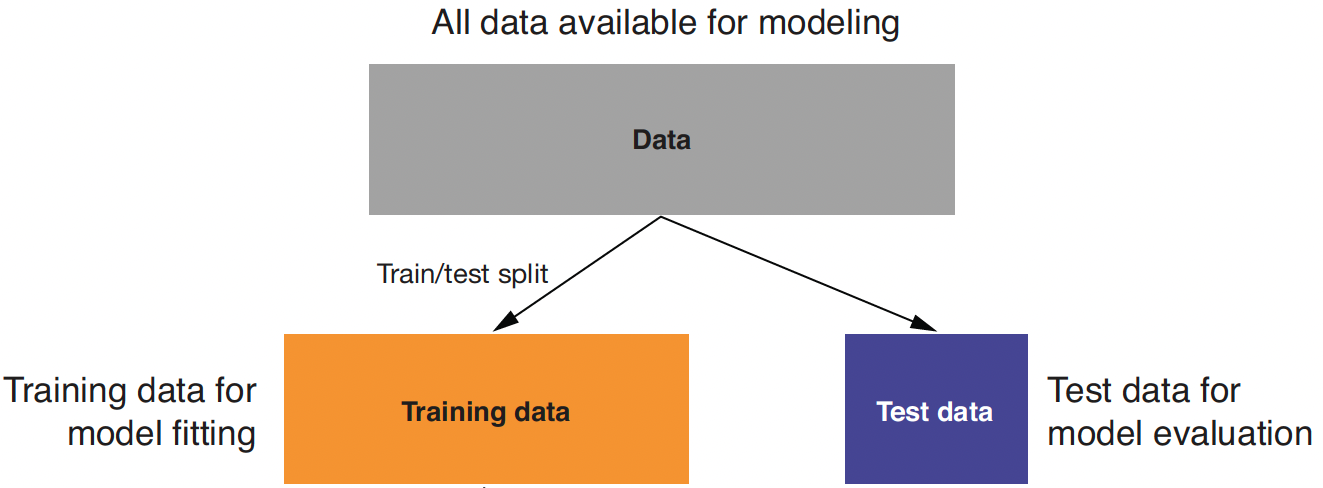
Evaluating Models

  • Training data: When we're building a model to make predictions or to identify the relationships, we need data to build the model.

  • Testing data: We also need data to test whether the model works well on new data.

  • So, we split data into training and test sets when building a linear regression model.

7 / 37

Linear Regression using R

8 / 37

Linear Regression

Example of Linear Regression using R

  • Let's use the 2016 US Census PUMS dataset.

    • Full-time employees between 20 and 50 years of age with income between $1,000 and $250,000;

  • Personal data recorded includes personal income and demographic variables:

    • PINCP: personal income
    • AGEP: age
    • SEX: sex
9 / 37

Linear Regression

Spliting Data into Training and Testing Data

# Importing the cleaned small sample of data
psub <- readRDS( url('https://bcdanl.github.io/data/psub.RDS') )
# Making the random sampling reproducible by setting the random seed.
set.seed(3454351) # 3454351 is just any number.
# The set.seed() function sets the starting number 
# used to generate a sequence of random numbers.
# With set.seed(), we can replicate the random number generation:
# If we start with that same seed number in the set.seed() each time, 
# we run the same random process, 
# so that we can replicate the same random numbers.
# How many random numbers do we need?
gp <- runif( nrow(psub) ) 
# a number generation from a random variable that follows Unif(0,1)
# Splits 50-50 into training and test sets 
# using filter() and gp
dtrain <- filter(psub, gp >= .5) 
dtest <- filter(psub,  gp < .5)
# A vector can be used for CONDITION in the filter(data.frame, CONDITION) 
# if the length of the vector is the same as that of the data.frame.
10 / 37

Linear Regression

Exploratory Data Analysis (EDA)

  • Use summary statistics and visualization to explore the data, particularly for the following variables:

    • PINCP: personal income
    • AGEP: age
    • SEX: sex
  • It's often a better idea to get some sense of how the data behaves through EDA before doing any statistical analysis.
# install.packages("GGally")  # to use GGally::ggpairs()
ggpairs( select(dtrain, PINCP, AGEP, SEX) )  # for correlogram or correlation matrix
11 / 37

Linear Regression

Building a linear regression model using lm()

model <- lm(formula = PINCP ~ AGEP + SEX, 
            data = dtrain)

In the above line of R commands, ...

  • model: R object to save the estimation result of linear regression
  • lm(): Linear regression modeling function
  • PINCP ~ AGEP + SEX: Formula for linear regression
  • PINCP: Outcome/Dependent variable
  • AGEP, SEX: Input/Independent/Explanatory variables
  • dtrain: Data frame to use for training
12 / 37

Linear Regression using R

Making predictions with a linear regression model using predict()

dtest$pred <-  predict(model, 
                       newdata = dtest)
  • In the above line of R commands, ...
    • dtest$pred: Adding a new column pred to the dtest data frame. mutate() also works.
    • predict(): Function to get the predicted outcome using model and dtest
    • model: R object to save the estimation result of linear regression
    • dtest: Data frame to use in prediction
  • We can make prediction using dtrain data frame too.
13 / 37

Linear Regression using R

Summary of the regression result

summary(model)   # This produces the output of the linear regression.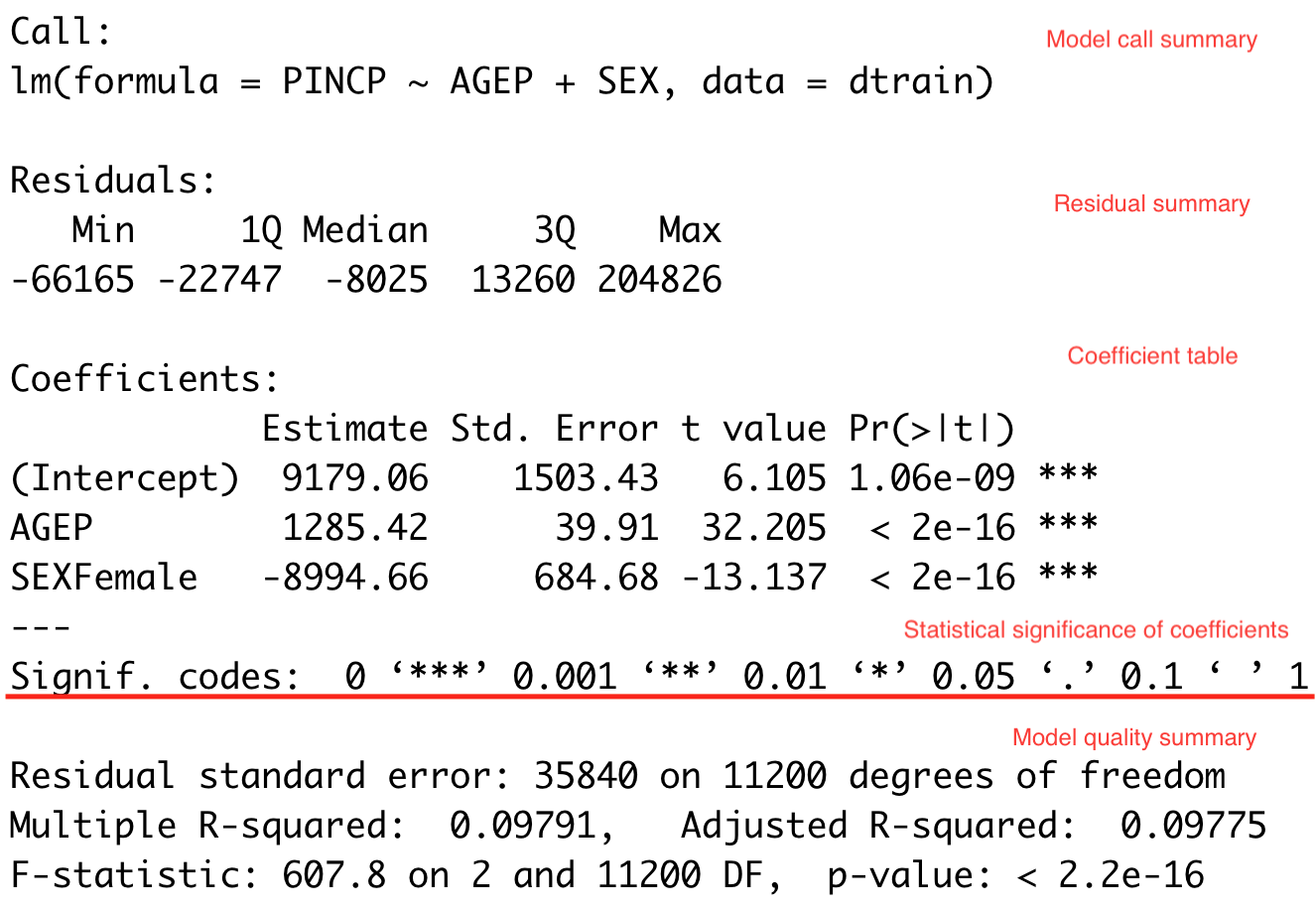

14 / 37

Linear Regression using R

Getting Estimates of Beta Coefficients

  • coef() returns the beta estimates:
coef(model)   
coef(model)['AGEP']
15 / 37

Linear Regression using R

Indicator variables

  • Linear regression handles a factor variable with m possible levels by converting it to m-1 indicator variables, and the rest 1 category, the first level of the factor variable, becomes a reference level.

  • The value of any indicator variable is either 0 or 1.

  • E.g., the indicator variable, SEXFemale, is follows:

SEXFemale[i]  ={1if a person i is female;0otherwise.

  • The level male becomes a reference level when interpreting the beta estimate for SEXFemale.
16 / 37

Linear Regression using R

Setting a reference level

  • If the independent variable includes factor variables, we can set a reference level for each factor variable using relevel(VARIABLE, ref = "LEVEL").
dtrain$SEX <- relevel(dtrain$SEX, ref = "Female") 
model <- lm(PINCP ~ AGEP + SEX, 
            data = dtrain)
summary(model)
  • E.g., the indicator variable, SEXMale, is follows:

SEXMale[i]  ={1if a person i is male;0otherwise.

  • The level Female now becomes a reference level.

  • Note: Changing the reference level does not change the regression result.

17 / 37

Linear Regression using R

Interpreting Estimated Coefficients

The model is ...

PINCP[i]=b0+b1*AGEP[i]+b2*SEX.Male[i]+e[i]

All else being equal, ...

  • All else being equal, an increase in AGEP by one unit is associated with an increase in PINCP by b1.

  • All else being equal, an increase in SEX.Male by one unit is associated with an increase in PINCP by b2.

  • All else being equal, being a male relative to being a female is associated with an increase in PINCP by b2.

18 / 37

Linear Regression using R

Interpreting Estimated Coefficients

Consider the predicted incomes of the two male persons, Ben and Bob, whose ages are 51 and 50 respectively.

^PINCP[Ben]=^b0+^b1 * AGEP[Ben]+^b2 * SEX.Male[Ben]^PINCP[Bob]=^b0+^b1 * AGEP[Bob]+^b2 * SEX.Male[Bob]

⇔^PINCP[Ben]−^PINCP[Bob]=^b1 * (AGEP[Ben]−AGEP[Bob])=^b1 * (51 - 50)=^b1

19 / 37

Linear Regression using R

Interpreting Estimated Coefficients

Consider the predicted incomes of the two persons, Ben and Linda, whose ages are the same as 50. Ben is male and Linda is female.

^PINCP[Ben]=^b0+^b1 * AGEP[Ben]+^b2 * SEX.Male[Ben]^PINCP[Linda]=^b0+^b1 * AGEP[Linda]+^b2 * SEX.Male[Linda]

⇔^PINCP[Ben]−^PINCP[Linda]=^b2 * (SEX.Male[Ben]−SEX.Male[Linda])=^b2 * (1 - 0)=^b2

20 / 37

Linear Regression using R

Interpreting Estimated Coefficients

  • What does it mean for a beta estimate ˆb to be statistically significant at 5% level?

    • It means that the null hypothesis H0:b=0 is rejected for a given significance level 5%.

    • "2 standard error rule" of thumb: The true value of b is 95% likely to be in the confidence interval (ˆb−2∗Std. Error,ˆb+2∗Std. Error).

    • The standard error tells us how uncertain our estimate of the coefficient b is.

    • We should look for the stars!

21 / 37

Linear Regression using R

Interpreting Estimated Coefficients

  • Using the "2 standard error rule" of thumb, we could refine our earlier interpretation of beta estimates as follows:

    • All else being equal, an increase in AGEP by one unit is associated with an increase in PINCP by b1 ± 2*Std.Err.b1.

    • All else being equal, being a male relative to being a female is associated with an increase in PINCP by b2 ± 2*Std.Err.b2 .

22 / 37

Linear Regression using R

R-squared

  • R-squared is a measure of how well the model “fits” the data, or its “goodness of fit.”
    • R-squared can be thought of as what fraction of the y's variation is explained by the independent variables.
  • R-squared will be higher for models with more explanatory variables, regardless of whether the additional explanatory variables actually improve the model or not.
  • We want R-squared to be fairly large and R-squareds that are similar on testing and training.
  • The adjusted R-squared is the multiple R-squared penalized for the number of input variables.
23 / 37

Linear Regression using R

Visualizations to diagnose the quality of modeling results

  • The following two visualizations from the linear regression are useful to determine the quality of linear regression:

    1. Actual vs. predicted outcome plot;
    2. Residual plot.
  • The following is the actual vs predicted outcome plot.
ggplot( data = dtest, 
        aes(x = pred, y = PINCP) ) +
  geom_point( alpha = 0.2, color = "darkgray" ) +
  geom_smooth( color = "darkblue" ) +  
  geom_abline( color = "red", linetype = 2 )  # y = x, perfect prediction line

  • The following is the residual plot.

    • Residual[i] = y[i] - Predicted_y[i].
ggplot(data = dtest, 
       aes(x = pred, y = PINCP - pred)) +
  geom_point(alpha = 0.2, color = "darkgray") +
  geom_smooth( color = "darkblue" ) +   
  geom_hline( aes( yintercept = 0 ),  # perfect prediction 
              color = "red", linetype = 2) + 
  labs(x = 'Predicted PINCP', y = "Residual error")

  • From the plot of actual vs. predicted outcomes and the plot of residuals, we should ask the following two questions ourselves:

    • On average, are the predictions correct?
    • Are there systematic errors?

  • A well-behaved plot will bounce randomly and form a cloud roughly around the perfect prediction line.

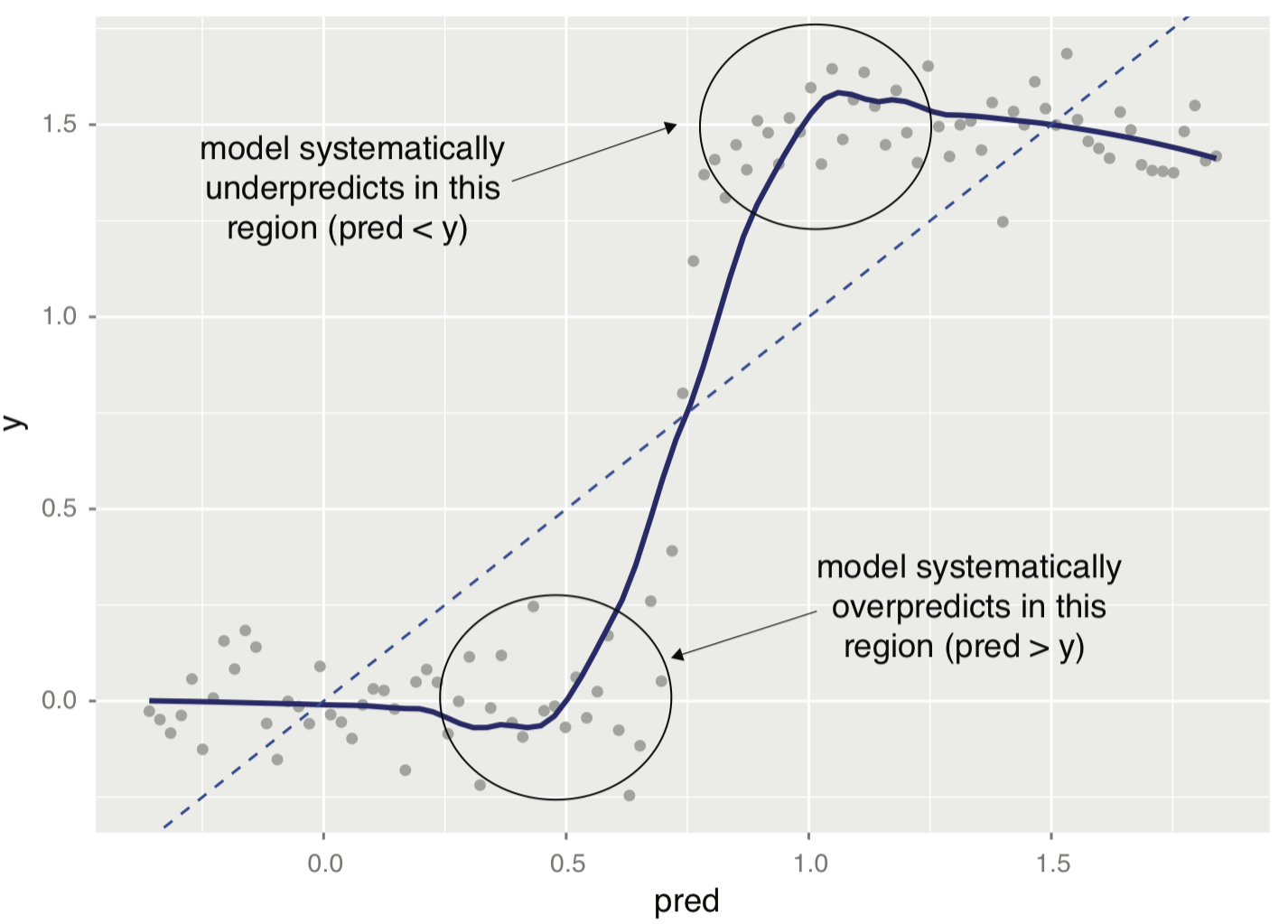
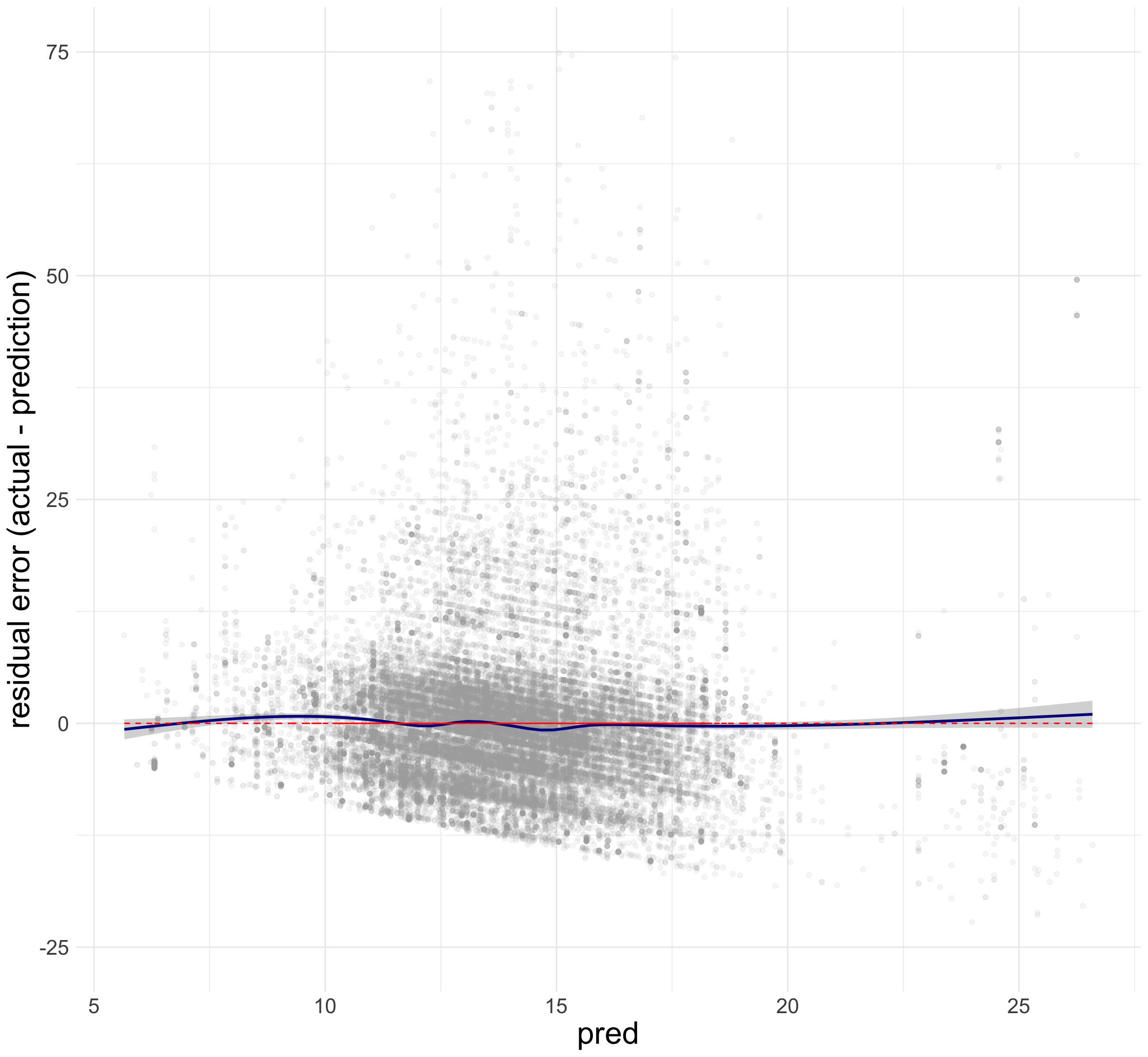
An example of systematic errors in model predictions

An example of systematic errors in model predictions

24 / 37

Linear Regression using R

Practical considerations in linear regression

  • Correlation does not imply causation:

    • Just because a coefficient is significant, doesn’t mean our explanatory variable causes the response of our outcome variable.

    • In order to test cause-and-effect relationships through regression, we would often need data from (quasi-)experiments to remove selection bias.

  • To achieve causality, researchers conduct experiments such as randomized controlled trials (RCT) and A/B testing:
    • The treatment group receives the treatment whose effect the researcher is interested in.
    • The control group receives either no treatment or a placebo.
    • The treatment variable indicates the status of treatment and control.
  • In linear regression, if all explanatory variables apart from the treatment variable are made equal across the two groups, selection bias is mostly eliminated, so that we may infer causality from beta estimates.

  • There is a difference between practical significance and statistical significance:

    • Whether an association between x and y is practically significant depends heavily on the unit of measurement.

    • E.g., We regressed income (measured in $) on height, and got a statistically significant beta estimate of 100, with a standard error of 20.

    • Q. Is 100 a large effect?

25 / 37

Linear Regression using R

More Explanatory Variables in the Model

  • In the 2016 US Census PUMS dataset, personal data recorded includes occupation, level of education, personal income, and many other demographic variables:

    • COW: class of worker
    • SCHL: level of education
26 / 37

Linear Regression using R

More Explanatory Variables in the Model

  • Suppose we also want to assess how personal income (PINCP) varies with (1) age (AGEP), and (2) gender (SEX), and (3) a bachelor's degree (SCHL).

    1. Conduct the exploratory data analysis.
    2. Based on the visualization, set a hypothesis regarding the relationship between having bachelor's degree and PINCP.
    3. Train the linear regression model.
    4. Interpret the beta coefficients from the linear regression result.
    5. Calculate the predicted PINCP using the testing data.
    6. Draw the actual vs. predicted outcome plot and the residual plot.
27 / 37

Linear Regression in R

The model equation

PINCP[i]=b0+b1*AGEP[i]+b2*SEX.Male[i]b3*SCHL.no high school diploma[i]+b4*SCHL.GED or alternative credential[i]+b5*SCHL.some college credit, no degree[i]+b6*SCHL.Associate's degree[i]+b7*SCHL.Bachelor's degree[i]+b8*SCHL.Master's degree[i]+b9*SCHL.Professional degree[i]+b10*SCHL.Doctorate degree[i]+e[i].

28 / 37

Linear Regression with Log-transformed Variables

29 / 37

Linear Regression with Log-transformtion

A Little Bit of Math for Logarithm

  • The logarithm function, y=logb(x), looks like ....

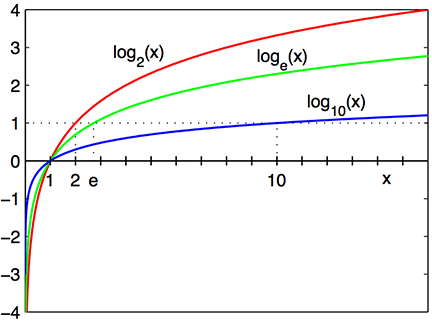
  • loge(x): the base e logarithm is called the natural log, where e=2.718⋯ is the mathematical constant, the Euler's number.

  • log(x) or ln(x): the natural log of x .

  • loge(7.389⋯): the natural log of 7.389⋯ is 2, because e2=7.389⋯.

30 / 37

Linear Regression with Log-transformtion

  • We should use a logarithmic scale when percent change, or change in orders of magnitude, is more important than changes in absolute units.

    • For small changes in variable x from x0 to x1, the following can be shown:

Δlog(x)=log(x1)−log(x0)≈x1−x0x0=Δxx0.

  • A difference in income of $5,000 means something very different across people with different income levels.

    • We should also consider using a log scale to reduce a variance of residuals when a variable is heavily skewed.
31 / 37

Linear Regression with Log-transformtion

  • The log transformation makes the skewed distribution of income more normal.
ggplot(dtrain, aes( x = PINCP ) ) +
  geom_density() 
ggplot(dtrain, aes( x = log(PINCP) ) ) +
  geom_density()
32 / 37

Linear Regression with Log-transformtion

log(PINCP[i])=b0+b1*AGEP[i]+b2*SEX.Male[i]b3*SCHL.no high school diploma[i]+b4*SCHL.GED or alternative credential[i]+b5*SCHL.some college credit, no degree[i]+b6*SCHL.Associate's degree[i]+b7*SCHL.Bachelor's degree[i]+b8*SCHL.Master's degree[i]+b9*SCHL.Professional degree[i]+b10*SCHL.Doctorate degree[i]+e[i].

33 / 37

Linear Regression with Log-transformtion

A Few Algebras for Logarithm and Exponential Functions

  • Rule 1: y=log(x)⇔exp(y)=x.
  • Rule 2:

log(x)−log(z)=log(xz).

  • By the rules above, log(x)−log(z)=b⇔xz=exp(b).
34 / 37

Linear Regression with Log-transformtion

Interpreting Beta Estimates

  • If we apply the rule above for Bob and Ben's predicted incomes,

⇔^log(PINCP[Ben])−^log(PINCP[Bob])=^b1 * (AGEP[Ben]−AGEP[Bob])=^b1 * (51 - 50)=^b1

So we can have the following: ⇔^PINCP[Ben]^PINCP[Bob]=exp(^b1)⇔^PINCP[Ben]=^PINCP[Bob]∗exp(^b1)

35 / 37

Linear Regression with Log-transformtion

Interpreting Beta Estimates

  • If we apply the rule above for Ben and Linda's predicted incomes,

^PINCP[Ben]^PINCP[Linda]=exp(^b2)⇔^PINCP[Ben]=^PINCP[Linda]∗exp(^b2)

  • Suppose exp(^b2)=1.18.

    • Then ^PINCP[Ben] is 1.18 times ^PINCP[Linda].

    • It means that being a male is associated with an increase in income by 18% relative to being a female.

36 / 37

Linear Regression with Log-transformtion

Interpreting Beta Estimates

  • All else being equal, an increase in AGEP by one unit is associated with an increase in log(PINCP) by b1.

  • All else being equal, an increase in AGEP by one unit is associated with an increase in PINCP by (exp(b1) - 1)%.

  • All else being equal, an increase in SEXMale by one unit is associated with an increase in log(PINCP) by b2.

  • All else being equal, being a male is associated with an increase in PINCP by (exp(b1) - 1)% relative to being a female.

37 / 37

Modeling Methods - Linear Regression

2 / 37
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow